CORTANTE EN VIGAS DE MADERA( Parte 1º , El fenómeno)

1 Introducción

En las comprobaciones de vigas de madera, el cortante suele ser olvidado y desconocido, quizás por qué raramente es origen de patologías resistentes. En las verificaciones de estados límite, las deformaciones suelen monopolizar la atención de los diseñadores, pero el cortante existe, y dada su falla que generalmente es frágil, no debemos rehuir de conocer y realizar correctamente las comprobaciones que lo rodean.

Exponemos aquí el fenómeno del esfuerzo cortante en vigas de madera maciza o productos ingenieriles derivados de la madera (laminada, microlaminada-LVL, partículas-LSL), y dejamos para la segunda parte de este artículo las distintas posibilidades de refuerzo para cortante.

2 La anisotropía de la madera y el cortante

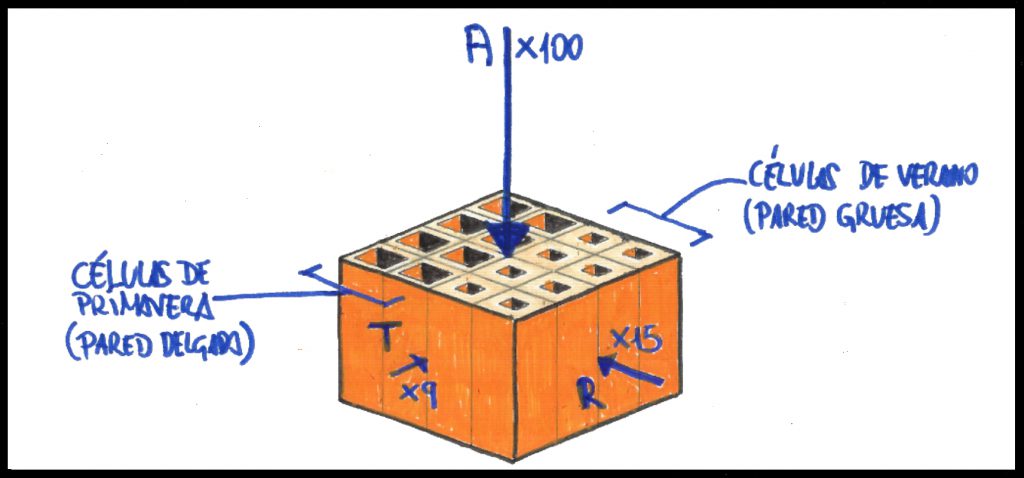
De acuerdo con la evolución natural de los árboles, un tronco se puede entender como un haz de células vegetales (llamadas traqueidas), que son como minúsculos tubos alargados que discurren en el sentido largo del tronco, y que se encargan de distribuir el alimento a todo el árbol.

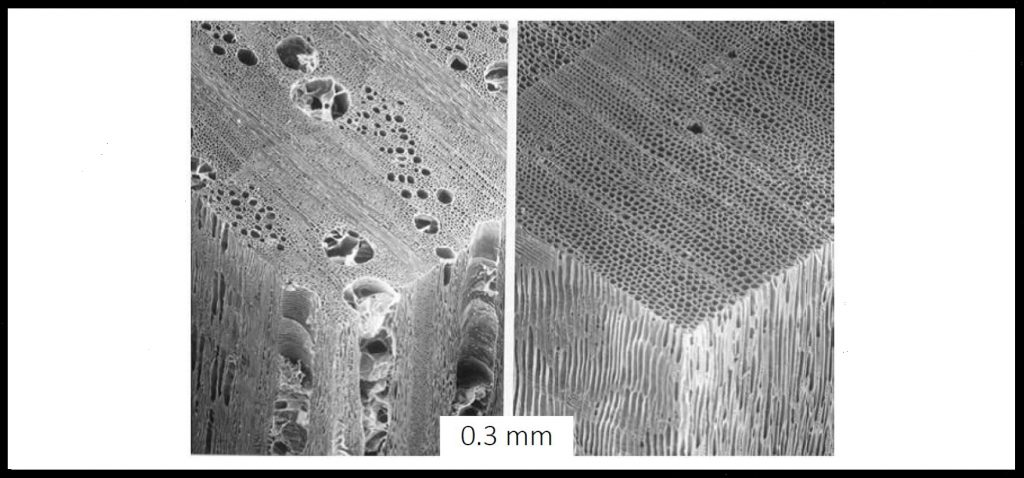
Esta característica de la madera que hace variar sus atributos físicos según la dirección en que se midan se denomina anisotropía, y resulta fundamental tenerla en cuenta dado que las propiedades mecánicas son distintas según la dirección del esfuerzo. Así, se consideran tres direcciones principales:

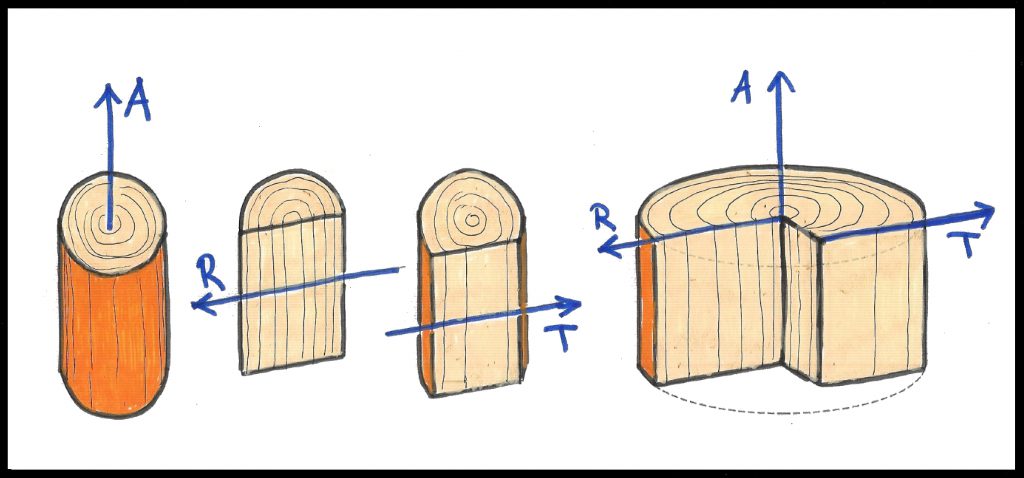
• Dirección axial (A), paralela al eje de crecimiento del árbol. Generada en ángulo recto con el eje del tronco y de sección circular, revelando duramen, albura y anillos anuales
• Dirección radial (R), perpendicular a la dirección axial y cortando el eje del árbol, divide el tallo longitudinalmente a través de la médula, similar a un segmento circular y muestra las células axiales y radiales. Aquí, las fibras corren horizontalmente y se pueden ver los anillos anuales
• Dirección tangencial (T), perpendicular a las dos anteriores, discurre tangencialmente a los anillos anuales, como un segmento circular. Los anillos anuales no se ven tan claramente en este caso, mientras que las células axiales son fácilmente visibles

Estos planos de sección natural de la madera surgen como resultado de la clara simetría axial y sección transversal redonda del tronco.

En resumen: es más fácil romper la madera separando las células entre sí (perpendicularmente al sentido largo del tronco), que cortándolas.

En madera maciza y laminada encolada, la resistencia a cortante paralela a la fibra es considerablemente menor que la perpendicular, en cuyo caso habría que cortar las fibras en caso de fractura por cortante. Por consiguiente, el cortante paralelo a la fibra (cortante longitudinal) es decisivo para el diseño.

Esto se refleja en la forma de partir leña que emplean los Aizkolaris (entre otros cortadores de madera): se ataca al tronco en sentido oblicuo, pues con un corte en sentido completamente transversal las células ofrecen mayor resistencia. En cambio, si se practicase un corte en el sentido completamente longitudinal según la dirección de las fibras (dirección radial), estas ofrecen la mínima resistencia, como si el tronco fuese un haz de fibras que se deshilachan.

https://www.eitb.eus/es/deportes/otrosdeportes/videos/detalle/7702427/video-sherpaai-aizkolari-txapelketa-iker-vicente-campeon-segundo-ano/ (a partir del segundo 17″)

3 Cómo se comporta la madera a cortante

El cortante es un esfuerzo interno de los elementos estructurales que resulta generalmente de las tensiones paralelas a su sección transversal. De acuerdo con la teoría de la elasticidad, los esfuerzos cortantes se generan cuando la flexión es producida por cargas perpendiculares al eje de la viga (que equivale a la dirección longitudinal del tronco en el caso de la madera).

Al trasladar la anisotropía de la madera al esfuerzo cortante y analizando la composición básica de las células que la componen, se hace patente que cuando aparece cortante, hay rasante (esfuerzo a lo largo de la viga que tiende a separar sus fibras deslizando unas sobre otras longitudinalmente), y dada la poca capacidad de la lignina para mantener las células unidas, por lo general la falla en realidad es por rasante: se manifiesta según un desplazamiento relativo de las células, no una rotura de las mismas, dado que tal como vimos se requiere mayor esfuerzo para conseguir esto último.

Dicho de otro modo: es más fácil cortar en sentido axial que en el de la longitud de las fibras, de lo cual resultan los tres tipos principales de fallo por cortante en la madera:

• Cortadura
• Deslizamiento
• Rodadura (que resulta más significativo en CLT)

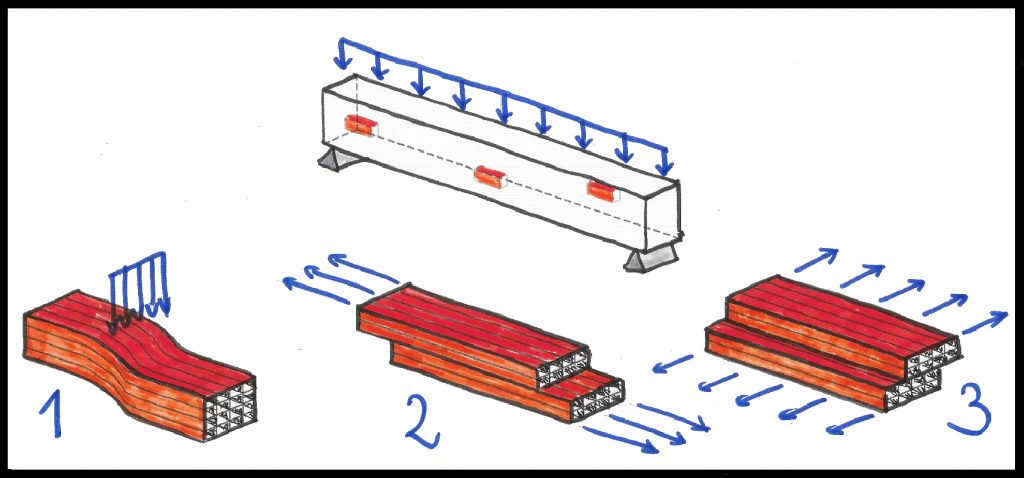
Luego el cortante afecta a nivel de tracciones perpendiculares a la fibra, siendo posible el fallo a cortante antes que por tracción paralela a fibras, donde la madera tiene mejores propiedades mecánicas.

En general, una viga de madera laminada, correctamente dimensionada a flexión, (y sin entalladuras ni huecos, que analizaremos más adelante), cumple sin mayor problema para el cortante, y es en aquellos casos en los que la luz es mayor de 9 veces el canto (L< 9h), en los que es posible el fallo por cortante.

4 Números gordos a cortante

Más allá de las consideraciones sobre anisotropía hechas anteriormente, las cuales tienen además repercusión en la deformación de las vigas en flexión (no entraremos en ello aquí), según el CTE-Madera, en el análisis de estructuras compuestas por barras, para el cálculo de solicitaciones globales de cortante, se considera válida la hipótesis de que el material es isótropo, elástico y lineal, según la teoría de vigas elásticas de Euler y Bernouilli, de acuerdo con la cual se puede deducir el esfuerzo cortante Tau en cualquier punto de la sección transversal, el cual para una sección rectangular toma una distribución en forma de parábola que alcanza su punto máximo en la fibra neutra, como se muestra en la figura:

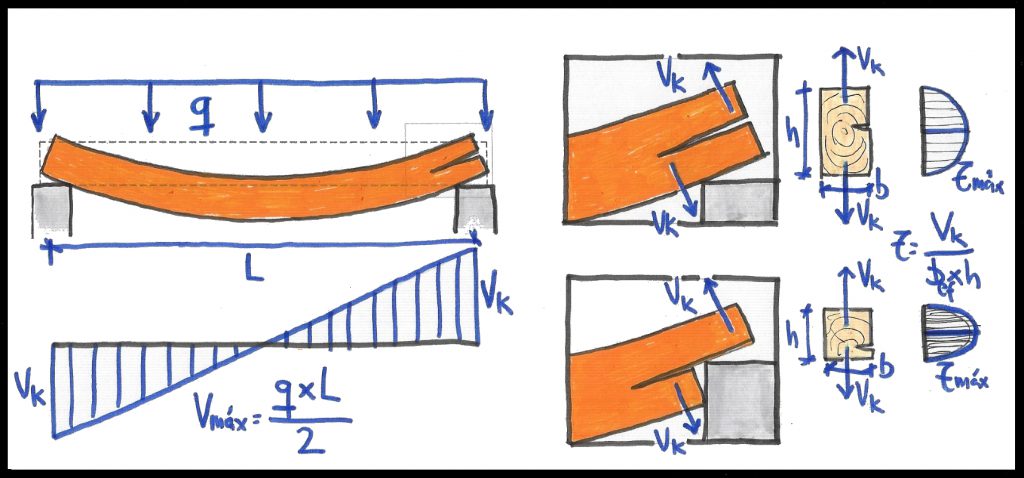
En este caso, las tensiones son perpendiculares a la fibra y el valor máximo de Tau es:

τ = [3 / 2] • [V / A]

Así, se debe comprobar que se cumple la siguiente ecuación:

τ = [3 / 2] • [V / A_ef] < f_v,d = [f_v,k/γ_M]• k_mod

dónde:

V, es el esfuerzo cortante de la viga

A_ef, es el área de la sección transversal

f_v,d, es la resistencia de cálculo

f_v,k, es la resistencia característica. Ver tabla de resistencias más adelante

γ_M, es el coeficiente de minoración del material, 1,30 para madera maciza, 1,25 para laminada, 1,20 para microlaminada o LSL

k_mod, es un coeficiente que depende de la duración de la carga y clase de servicio

Las fendas que pueda tener la madera suponen una pérdida de sección, lo cual tiene una incidencia directa en las tensiones por cortante. Así, debe tenerse en cuenta su influencia negativa en la resistencia a cortante de las vigas, por lo que el área A_ef se determina a partir de un ancho de viga reducido, llamado ancho efectivo b_ef, según la expresión:

b_ef = b • k_cr

Siendo k_cr un coeficiente que depende del material. Para madera maciza y laminada encolada se considera k_cr=0,67, y en el caso de maderas microlaminadas o LSL, puede considerarse libres de grietas o fendas, y en este caso el factor k_cr puede utilizarse como 1,0.

A efectos de tener orden de magnitud de las resistencias, se resumen algunos valores para distintos productos. Se puede ver que las resistencias en la dirección de las fibras son claramente mayores a las que se refieren a la dirección perpendicular.

(Valores en MPa)		GL24h	C24	LVL	LSL
Tracción paralela	ft,0,k	16.5	14	22	29,1
Tracción perpendicular	ft,0,k	0,4	0,4	—	0,66
Compresión paralela	fc,0,k	24	22	21	29
Compresión perpendicular	fc,90,k	2,7	2,5	9	8,7
Cortante	fv,k	2,7	4,0	4,5	8,6

Zonas con rebaje de la sección en apoyos o huecos

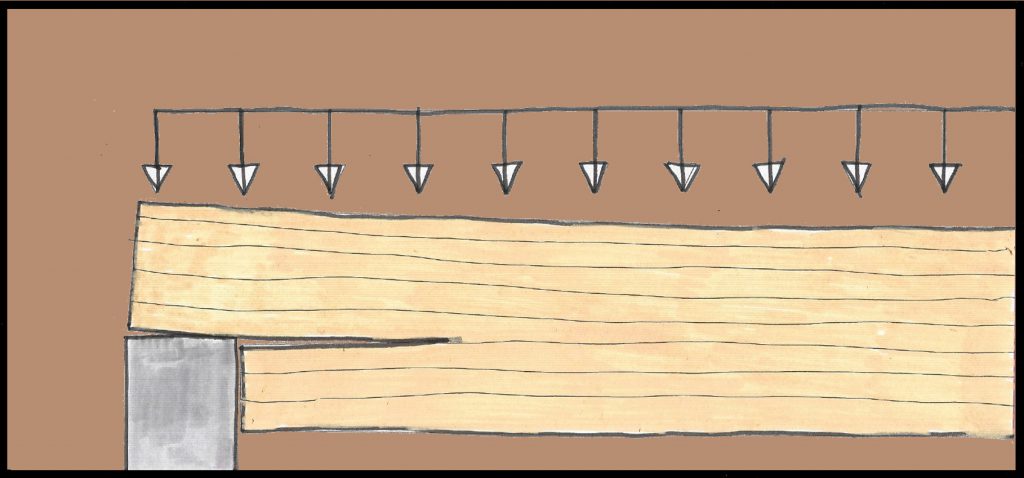
Como vimos, en vigas con los extremos rebajados, especialmente con ángulos poco suavizados en el cambio de sección, debe tenerse en cuenta la influencia de la concentración de tensiones oblicuas respecto la fibra, que solicitan a la viga por encima de las habituales. Para las vigas de sección rectangular con la fibra sensiblemente paralela al eje, esta influencia se considera haciendo la comprobación siguiente:

τ_s = [3 / 2] • [V_d / b • h_ef] > k_v • f_vd

siendo:

V_d, esfuerzo cortante de cálculo en la viga

h_ef , el canto eficaz

k_v, factor de reducción que depende de la transmisión de cargas en el apoyo (ver EC-5)

Repetimos que, a pesar de que no es muy frecuente, uno de los motivos por los que es importante no olvidar el cortante es que su fallo suele implicar una rotura frágil; es decir, no hay avisos como deformaciones o grietas de que la madera está cerca de su límite de rotura, con lo cual factores como ligeros incrementos de carga, pequeños asientos, gradiente térmico, etc., pueden suponer la «gota que colma el vaso» haciendo superar la tensión que la madera puede soportar, generando una grieta que por lo general reduce más la sección, agravando así la situación con gran riesgo de colapso.

Ante cualquier sospecha de una situación similar a esta, se deben tomar medidas como apuntalar, descargar, y analizar correctamente la situación.

La viabilidad y necesidad de refuerzo en una viga de madera con entalladuras o huecos depende de
múltiples factores como la luz, cargas, relación ancho/canto, geometría del rebaje, fuego, de manera que
resulta complejo dar recetas generales, así que no hay que dejar de comprobar el cortante, considerando
además de la propia entalladura o hueco, las reducciones de sección por taladros o rebajes para pletinas
habituales en los apoyos.

Igualmente, en zonas con agujeros, la verificación de la resistencia a cortante se basa en la comprobación de una viga equivalente con una entalladura, según se ilustra en la figura:

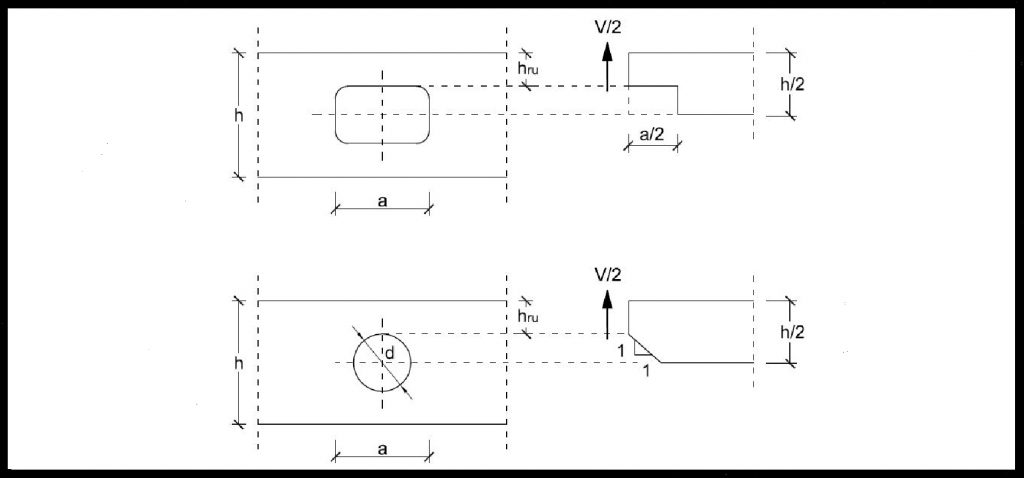
Además de la anisotropía y las reducciones de sección, otros factores que influyen en el comportamiento a cortante son las irregularidades de la madera como nudos o fendas, la calidad de la madera, el tamaño de las lamas o el adhesivo en productos encolados.

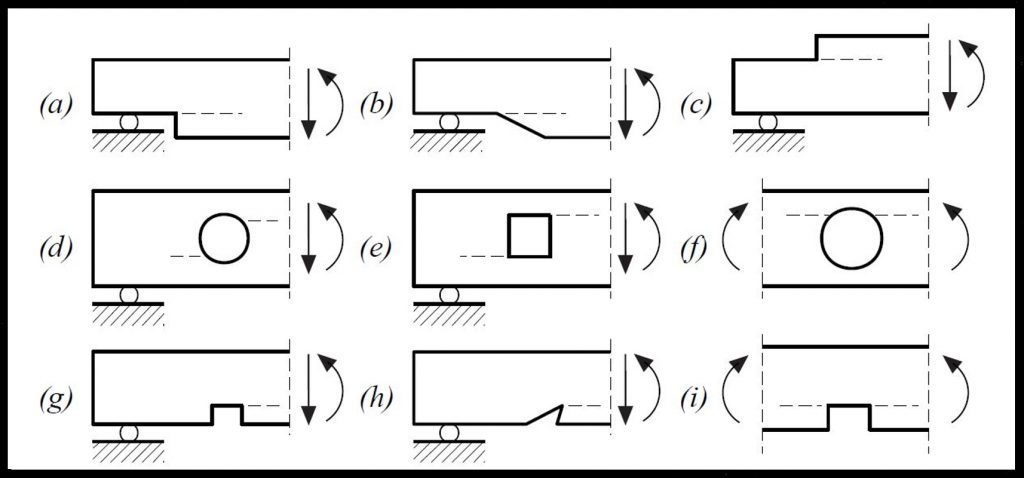
5 Terminamos con una pregunta

Para comprobar si hemos explicado suficientemente bien cómo funciona el cortante, sabrías decir, para igual sección, luz, carga y clase resistente de madera, ¿Cuál de estas dos ménsulas rompe antes a cortante? (se considera el muro infinitamente rígido y estable)

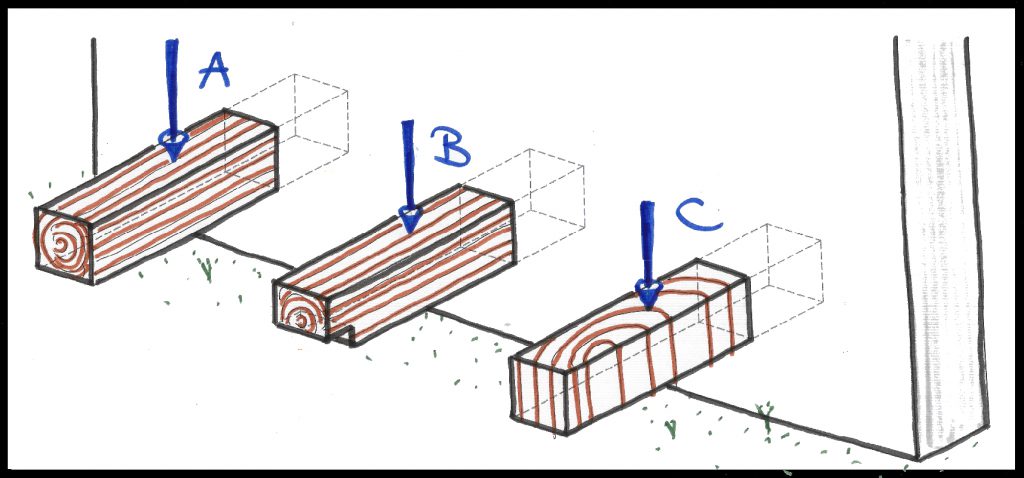
6 Fuentes bibliográficas

[1] Hans Joachim Blaβ et al.: «Timber Engineering STEP 1», Centrum Hout, Almere, 1995.

[2] Argüelles Álvarez, R., Arriaga, F., Esteban, M., Íñiguez-González, G. y Argüelles Bustillo, R. «Estructuras de madera. Bases de cálculo». Editorial AITIM, Madrid, 2013.

[3] Pascual Urbán Brotóns «Construcción. Estructuras de madera», Editorial Club Universitario, Alicante, 2012.

[4] Pablo Guindos, «Fundamentos del diseño y la construcción en madera», Editorial Universidad Católica de Chile, Santiago de Chile, 2019.

[5] Hans Joachim Blaβ, Carmen Sandhaas, «Timber Engineering. Principles for Design», Karlsruher Institut für Technologie, Karlsruhe, 2017.

[6] Hans Joachim Blaβ, Johannes Streib, «BauBuche Beech LVL. Manual for design and structural calculation in accordance with Eurocode», Pollmeier Massivholz GmbH & Co.KG, Creuzburg, 2019.

[7] UNE-EN 1995-1-1:2016 «Eurocódigo 5. Proyecto de estructuras de madera. Parte 1-1: Reglas generales. Reglas edificación», 2016.

[8] Real Decreto 732/2019, de 20 de diciembre, «Código Técnico de la Edificación, Documento Básico SE-M Seguridad estructural. Madera», 2019.